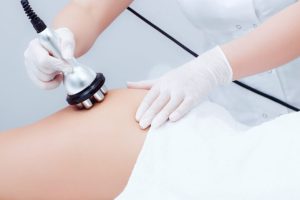
Коррекция фигуры является важной частью современных стремлений к идеальному телосложению, которое подчеркивает здоровье и
Термин «нишевый парфюм» произошел от французского понятия la niche и означает именно нишу в
Тайский масляный массаж осуществляется путем нанесения ароматических масел на тело, что способствует глубокому расслаблению
Стиль прованс, истоки которого уходят в живописные уголки Южной Франции, сегодня покоряет сердца ценителей
В процессе аюрведического массажа используются специальные масла, которые подбираются индивидуально для каждого клиента с
Покупка новой обуви – это всегда захватывающее событие. Особенно если речь идет о подготовке
Смас лифтинг – это инновационная процедура, которая позволяет улучшить контуры лица, уменьшить морщины и
CRM помогает устанавливать и контролировать задачи для сотрудников, отслеживать контакты с клиентами, что повышает
В 2024 году коллекция детской одежды для весенне-летнего сезона поражает своей яркостью, игривостью и
Применение увлажняющего крема требует определенных правил для достижения максимального эффекта. Наносить крем желательно после
Кератин – строительный материал волос. Шампуни с кератином восстанавливают, укрепляют, придают блеск и защищают
Отличительной чертой онлайн обучения является его доступность и гибкость, что делает его идеальным для
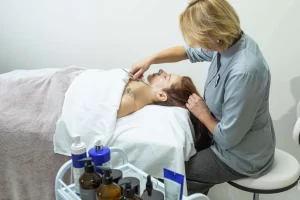
Уходовая косметология играет важную роль в поддержании здоровья и красоты кожи. Она представляет собой
Стимуляция овуляции является важным этапом в процессе ЭКО (экстракорпорального оплодотворения), который помогает женщинам
Парикмахерские ножницы – это не просто инструмент, а основа для создания идеальных стрижек и
Специалисты массажного салона обладают необходимыми навыками и знаниями для проведения различных видов массажа, начиная
Современные свадебные торжества зачастую представляют собой сложные события с множеством деталей: от выбора места
Вы хотите продвинуть свой сайт и привлечь больше посетителей? Тогда вы понимаете, что раскрутка
Выбор пептидных препаратов должен быть осознанным и обоснованным. Перед началом приема любого препарата необходимо
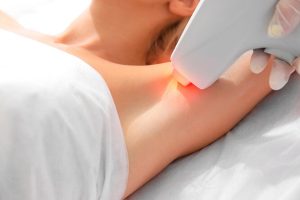
Диодная лазерная эпиляция – это современная и эффективная методика удаления нежелательных волос, которая становится
В отличие от обычных средств, доступных в массовом рынке, профессиональная косметика разработана с учетом
Свадебные костюмы могут варьироваться от классических и традиционных до более современных и нестандартных моделей.
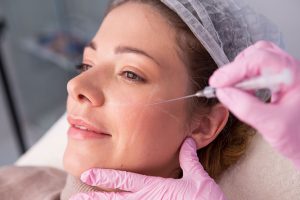
Биоревитализация запускает повышение тонуса дермы, выработку белков. Неэстетичные участки с обвисшей кожей подтягиваются, приобретают
В мире строительства и инженерии существует постоянная потребность в эффективных и долговечных системах, способных
Следуя вышеперечисленным советам, вы сможете найти лучшие предложения, экономя время и деньги при покупках
СМАС-лифтинг (Superficial Muscular Aponeurotic System) – это современная методика аппаратного лифтинга, предназначенная для улучшения
СМАС-лифтинг — это хирургическая процедура, при которой врач работает не только с кожными покровами,